FORM+CODE In Design, Art, and Architecture by Casey Reas, Chandler McWilliams, and LUST

Visualize: SUPERFORMULA

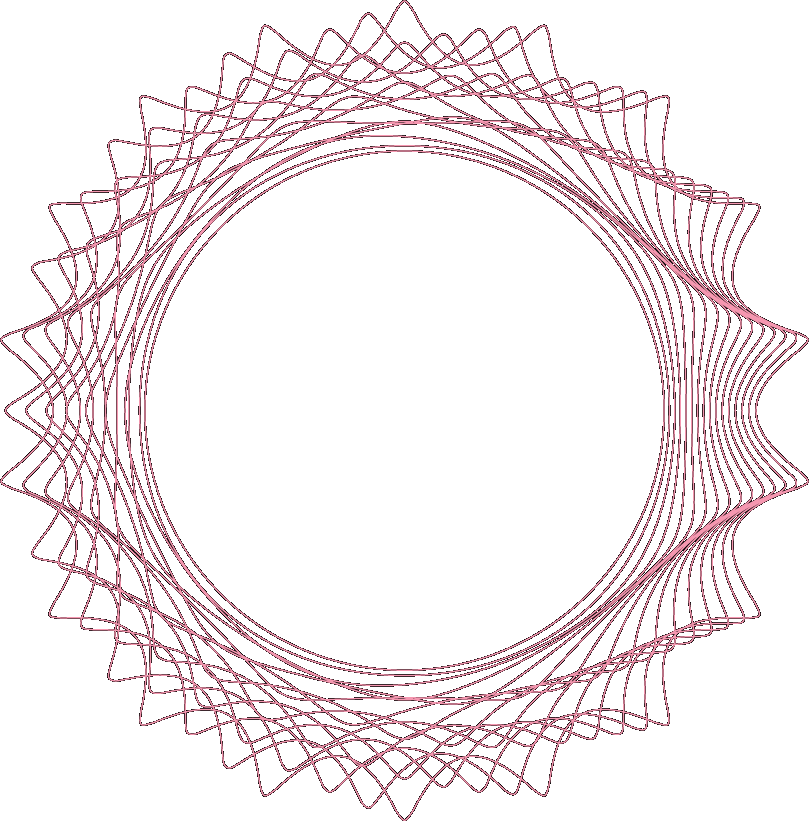
The superformula was first described by Johan Gielis in 2003 as a way to mathematically generate a wide variety of forms found in nature. The form generated by the equation can be controlled by setting the values of a few key parameters. The verdict is still out as to whether the superformula actually describes processes in nature or simply produces a good imitation of them.

The first step to create a basic 2-D form based on the superformula is to set the values for the parameters named m, n1, n2, and n3. The m parameter changes the number of petals on the final form, and the n parameters affect the shape and size of the petals. The equation for the superformula is based on a circle. Finding the position of each point in the final form requires iterating around the degrees of a circle, from 0 to 359, and plugging the angle and parameters into the equation.


/**
 * Visualize: Superformula
 * from Form+Code in Design, Art, and Architecture 
 * by Casey Reas, Chandler McWilliams, and LUST
 * Princeton Architectural Press, 2010
 * ISBN 9781568989372
 * 
 * This code was written for Processing 1.2+
 * Get Processing at http://www.processing.org/download
 */

float scaler = 200;
int m = 2;
float n1 = 18;
float n2 = 1;
float n3 = 1;

void setup() {
  size(700, 700);
  smooth();
  noFill();
  stroke(255);
}

void draw() {
  background(0);
  
  pushMatrix();
  translate(width/2, height/2);

  float newscaler = scaler;
  for (int s = 16; s > 0; s--) {  
    beginShape();
  
    float mm = m + s;
    float nn1 = n1 + s;
    float nn2 = n2 + s;
    float nn3 = n3 + s;
    newscaler = newscaler * 0.98;
    float sscaler = newscaler;

    PVector[] points = superformula(mm, nn1, nn2, nn3);
    curveVertex(points[points.length-1].x * sscaler, points[points.length-1].y * sscaler);
    for (int i = 0;i < points.length; i++) {
      curveVertex(points[i].x * sscaler, points[i].y * sscaler);
    }
    curveVertex(points[0].x * sscaler, points[0].y * sscaler);
    endShape();
  }
  popMatrix();
}


PVector[] superformula(float m,float n1,float n2,float n3) {
  int numPoints = 360;
  float phi = TWO_PI / numPoints;
  PVector[] points = new PVector[numPoints+1];
  for (int i = 0;i <= numPoints;i++) {
    points[i] = superformulaPoint(m,n1,n2,n3,phi * i);
  }
  return points;
}

PVector superformulaPoint(float m,float n1,float n2,float n3,float phi) {
  float r;
  float t1,t2;
  float a=1,b=1;
  float x = 0;
  float y = 0;

  t1 = cos(m * phi / 4) / a;
  t1 = abs(t1);
  t1 = pow(t1,n2);

  t2 = sin(m * phi / 4) / b;
  t2 = abs(t2);
  t2 = pow(t2,n3);

  r = pow(t1+t2,1/n1);
  if (abs(r) == 0) {
    x = 0;
    y = 0;
  }  
  else {
    r = 1 / r;
    x = r * cos(phi);
    y = r * sin(phi);
  }

  return new PVector(x, y);
}

Contributed Examples

ActionScript

view

/**
 * Visualize: Superformula from Form+Code in Design, Art, and Architecture 
 * implemented in ActionScript 3 by Ben Rubin <blog.benjaminrubin.com>
 * 
 * Run from the command line with: mxmlc Superformula.as
 * Mxmlc is available free as part of the Flex SDK: http://opensource.adobe.com/wiki/display/flexsdk/Flex+SDK
 *	
 * For more information about Form+Code visit http://formandcode.com
 */
package 
{
  import flash.display.GraphicsPath;
  import flash.display.GraphicsSolidFill;
  import flash.display.GraphicsStroke;
  import flash.display.IGraphicsData;
  import flash.display.Shape;
  import flash.display.Sprite;
  import flash.events.Event;
  import flash.geom.Point;
  import flash.text.TextField;
  import rubin.ui.Slider;
  
  public class Main extends Sprite 
  {
    
    public function Main():void 
    {
      if (stage) init();
      else addEventListener(Event.ADDED_TO_STAGE, init);
    }
    
    private var scaler:Number = 200;
    private var m:int = 2;
    private var n1:Number = 18;
    private var n2:Number = 4;
    private var n3:Number = 2;
    
    private static const TWO_PI:Number = Math.PI * 2;
    
    private var shape:Shape;
    
    
    private function init(e:Event = null):void 
    {
      removeEventListener(Event.ADDED_TO_STAGE, init);
      // entry point
      
      shape = new Shape();
      shape.x = stage.stageWidth / 2;
      shape.y = stage.stageHeight / 2;
      stage.addChild(shape);
      
      var scalerTitle:TextField = new TextField();
      scalerTitle.text = "Scaler";
      scalerTitle.textColor = 0xFF80C0;
      scalerTitle.x = 10;
      scalerTitle.y = 10;
      this.addChild(scalerTitle);
      
      var scalerSlider:Slider = new Slider();
      scalerSlider.min = 150;
      scalerSlider.max = 300;
      scalerSlider.minRange = 150;
      scalerSlider.maxRange = 300;
      scalerSlider.value = scaler;
      scalerSlider.x = 80;
      scalerSlider.y = 10;
      this.addChild(scalerSlider);
      scalerSlider.addEventListener(Event.CHANGE, scalerChange);
      
      var mTitle:TextField = new TextField();
      mTitle.text = "M";
      mTitle.textColor = 0xFF80C0;
      mTitle.x = 10;
      mTitle.y = 30;
      this.addChild(mTitle);
      
      var mSlider:Slider = new Slider();
      mSlider.min = -20;
      mSlider.max = 50;
      mSlider.minRange = -20;
      mSlider.maxRange = 50;
      mSlider.value = m;
      mSlider.x = 80;
      mSlider.y = 30;
      this.addChild(mSlider);
      mSlider.addEventListener(Event.CHANGE, mChange);
      
      var n1Title:TextField = new TextField();
      n1Title.text = "N1";
      n1Title.textColor = 0xFF80C0;
      n1Title.x = 10;
      n1Title.y = 50;
      this.addChild(n1Title);
      
      var n1Slider:Slider = new Slider();
      n1Slider.min = -10;
      n1Slider.max = 100;
      n1Slider.minRange = -10;
      n1Slider.maxRange = 100;
      n1Slider.value = n1;
      n1Slider.x = 80;
      n1Slider.y = 50;
      this.addChild(n1Slider);
      n1Slider.addEventListener(Event.CHANGE, n1Change);
      
      var n2Title:TextField = new TextField();
      n2Title.text = "N2";
      n2Title.textColor = 0xFF80C0;
      n2Title.x = 10;
      n2Title.y = 70;
      this.addChild(n2Title);
      
      var n2Slider:Slider = new Slider();
      n2Slider.min = -10;
      n2Slider.max = 100;
      n2Slider.minRange = -10;
      n2Slider.maxRange = 100;
      n2Slider.value = n2;
      n2Slider.x = 80;
      n2Slider.y = 70;
      this.addChild(n2Slider);
      n2Slider.addEventListener(Event.CHANGE, n2Change);
      
      var n3Title:TextField = new TextField();
      n3Title.text = "N3";
      n3Title.textColor = 0xFF80C0;
      n3Title.x = 10;
      n3Title.y = 90;
      this.addChild(n3Title);
      
      var n3Slider:Slider = new Slider();
      n3Slider.min = -10;
      n3Slider.max = 200;
      n3Slider.minRange = -10;
      n3Slider.maxRange = 200;
      n3Slider.value = n3;
      n3Slider.x = 80;
      n3Slider.y = 90;
      this.addChild(n3Slider);
      n3Slider.addEventListener(Event.CHANGE, n3Change);
      
      draw();
    }
    
    private function draw():void {
      shape.graphics.clear();
      shape.graphics.lineStyle(1, 0xFF80C0, 1);
      
      var newscaler:Number = scaler;
      var i:int;
      for (i = 16; i > 0; i--) {
        var mm:Number = m + i;
        var nn1:Number = n1 + i;
        var nn2:Number = n2 + 1;
        var nn3:Number = n3 + i;
        newscaler *= 0.98;
        var sscaler:Number = newscaler;
        
        var graphicsData:Vector.<IGraphicsData> = new Vector.<IGraphicsData>();
        
        var points:Vector.<Point> = superFormula(mm, nn1, nn2, nn3);
        
        var commands:Vector.<int> = new Vector.<int>();
        commands.push(1);
        var data:Vector.<Number> = new Vector.<Number>();
        data.push(points[points.length - 1].x * sscaler, points[points.length - 1].y * sscaler);
        
        var point:Point;
        for each(point in points) {
          commands.push(2);
          data.push(point.x * sscaler, point.y * sscaler);
        }
        
        graphicsData.push(new GraphicsPath(commands, data));
        shape.graphics.drawGraphicsData(graphicsData);
      }
    }
    
    private function superFormula(_m:Number, _n1:Number, _n2:Number, _n3:Number):Vector.<Point> {
      var numPoints:int = 360;
      var phi:Number = TWO_PI / numPoints;
      var points:Vector.<Point> = new Vector.<Point>();
      var i:int;
      for (i = 0; i < numPoints; i++) {
        points[i] = superformulaPoint(_m, _n1, _n2, _n3, phi * i);
      }
      
      return points;
    }
    
    private function superformulaPoint(_m:Number, _n1:Number, _n2:Number, _n3:Number, _phi:Number):Point {
      var r:Number;
      var t1:Number;
      var t2:Number;
      var a:Number = 1;
      var b:Number = 1;
      var x:Number = 0;
      var y:Number = 0;
      
      t1 = Math.cos(_m * _phi / 4) / a;
      t1 = t1 < 0 ? -t1:t1;
      t1 = Math.pow(t1, n2);
      
      t2 = Math.sin(_m * _phi / 4) / b;
      t2 = t2 < 0 ? -t2:t2;
      t2 = Math.pow(t2, _n3);
      
      r = Math.pow((t1 + t2), (1 / _n1));
      if (Math.abs(r) == 0) {
        x = 0;
        y = 0;
      }else {
        r = 1 / r;
        x = r * Math.cos(_phi);
        y = r * Math.sin(_phi);
      }
      
      return new Point(x, y);
    }
    
    private function scalerChange(e:Event):void {
      scaler = e.target.value;
      draw();
    }
    
    private function mChange(e:Event):void {
      m = e.target.value;
      draw();
    }
    
    private function n1Change(e:Event):void {
      n1 = e.target.value;
      draw();
    }
    
    private function n2Change(e:Event):void {
      n2 = e.target.value;
      draw();
    }
    
    private function n3Change(e:Event):void {
      n3 = e.target.value;
      draw();
    }
  } 
}

OpenFrameworks

view

/**
 * Visualize: Superformula from Form+Code in Design, Art, and Architecture 
 * implemented in OpenFrameworks by Anthony Stellato <http://rabbitattack.com/> 
 * 
 * Requires OpenFrameworks available at http://openframeworks.cc/
 *
 * For more information about Form+Code visit http://formandcode.com
 */

// ===========================================================
// - Visualize_Superformula.h
// ===========================================================
#include "ofMain.h"

class testApp : public ofBaseApp{

  public:
    void setup();
    void draw();

    ofPoint* superformula(float m, float n1, float n2, float n3);
    ofPoint superformulaPoint(float m, float n1, float n2, float n3, float phi);
};


// ===========================================================
// - Visualize_Superformula.cpp
// ===========================================================
#include "Visualize_Superformula.h"

float scaler = 200;
int m = 2;
float n1 = 18;
float n2 = 1;
float n3 = 1;
static int POINTNUM = 360;


void testApp::setup(){
  ofEnableSmoothing();
  ofNoFill();
  ofSetColor(255, 255, 255);
  
}


ofPoint testApp::superformulaPoint(float m, float n1, float n2, float n3, float phi)
{
  float r;
  float t1,t2;
  float a=1,b=1;
  float x = 0;
  float y = 0;
  
  t1 = cos(m * phi / 4) / a;
  t1 = fabs(t1);
  t1 = pow(t1,n2);
  
  t2 = sin(m * phi / 4) / b;
  t2 = fabs(t2);
  t2 = pow(t2,n3);
  
  r = pow(t1+t2,1/n1);
  if (fabs(r) == 0) {
    x = 0;
    y = 0;
  }  
  else {
    r = 1 / r;
    x = r * cos(phi);
    y = r * sin(phi);
  }
  return ofPoint(x, y);
}


ofPoint* testApp::superformula(float m, float n1, float n2, float n3)
{
  int numPoints = POINTNUM;
  float phi = TWO_PI / numPoints;
  ofPoint* retPoints = new ofPoint[numPoints+1];
  for(int i = 0; i <= numPoints; i++){
    retPoints[i] = superformulaPoint(m, n1, n2, n3, phi * i);
  }
  return retPoints;
}


void testApp::draw(){
  ofBackground(0, 0, 0);
  ofPushMatrix();
  ofTranslate(ofGetWidth()/2, ofGetHeight()/2, 0);
  
  float newscaler = scaler;
  for(int s = 16; s > 0; s--){
    ofBeginShape();
    
    float mm = m + s;
    float nn1 = n1 + s;
    float nn2 = n2 + s;
    float nn3 = n3 + s;
    newscaler = newscaler * 0.98;
    float sscaler = newscaler;
    
    ofPoint* points = superformula(mm, nn1, nn2, nn3);
    ofCurveVertex(points[POINTNUM-1].x * sscaler, points[POINTNUM-1].y * sscaler);
    for(int j = 0; j < POINTNUM; j++){
      ofCurveVertex(points[j].x * sscaler, points[j].y * sscaler);
    }
    ofCurveVertex(points[0].x * sscaler, points[0].y * sscaler);
    ofEndShape(true);
  }
  ofPopMatrix();
}

Cinder

view

/**
 * Visualize: Superformula from Form+Code in Art, Design, and Architecture
 * implemented in C++ by David Wicks <http://sansumbrella.com/>
 *
 * Requires Cinder 0.8.2 available at http://libcinder.org
 *
 * For more information about Form+Code visit http://formandcode.com
 */

#include "cinder/app/AppBasic.h"
#include "cinder/CinderMath.h"
#include "cinder/gl/gl.h"

using namespace ci;
using namespace ci::app;
using namespace std;

class Visualize_Superformula : public AppBasic {
public:
  void prepareSettings( Settings* settings );
  void setup();
  void draw();
  void calculateShape();
  vector<Vec2f> superformula( float m, float n1, float n2, float n3 );
  Vec2f superformulaPoint( float m, float n1, float n2, float n3, float phi );
private:
  Shape2d mSuperShape;
  float scaler;
  int   m;
  float n1, n2, n3;
};

void Visualize_Superformula::prepareSettings( Settings* settings )
{
  settings->setWindowSize( 700, 700 );
}

void Visualize_Superformula::setup()
{
  scaler = 200;
  m = 2;
  n1 = 18;
  n2 = 1;
  n3 = 1;
  
  calculateShape();
}

void Visualize_Superformula::draw()
{
  gl::clear( Color::black() ); 
  
  gl::pushMatrices();
  gl::translate( getWindowCenter() );
  
  gl::color( Color( CM_HSV, 0.9583f, 0.38f, 0.97f ) );
  gl::draw( mSuperShape );
  
  gl::popMatrices();
}

void Visualize_Superformula::calculateShape()
{
  float newscaler = scaler;
  
  for ( int s = 16; s > 0; s-- )
  {
    float mm = m + s;
    float nn1 = n1 + s;
    float nn2 = n2 + s;
    float nn3 = n3 + s;
    newscaler = newscaler * 0.98f;
    float sscaler = newscaler;
    
    vector<Vec2f> points = superformula( mm, nn1, nn2, nn3 );
    mSuperShape.moveTo( points[0] * sscaler );
    for( int i = 1; i < points.size(); i++ )
    {
      mSuperShape.quadTo( points[i-1] * sscaler, points[i] * sscaler );
    }
    
    mSuperShape.close();
  }
}

vector<Vec2f> Visualize_Superformula::superformula( float m, float n1, float n2, float n3 )
{
  int numPoints = 360;
  float phi = (M_PI * 2.0f) / numPoints;
  
  vector<Vec2f> points;
  for( int i = 0; i < numPoints; i++ )
  {
    points.push_back( superformulaPoint( m, n1, n2, n3, phi * i ) );
  }
  
  return points;
}

Vec2f Visualize_Superformula::superformulaPoint( float m, float n1, float n2, float n3, float phi )
{
  float r;
  float t1,t2;
  float a=1,b=1;
  float x = 0;
  float y = 0;
  
  t1 = cos(m * phi / 4) / a;
  t1 = abs(t1);
  t1 = pow(t1,n2);
  
  t2 = sin(m * phi / 4) / b;
  t2 = abs(t2);
  t2 = pow(t2,n3);
  
  r = pow(t1+t2,1/n1);
  if (abs(r) == 0)
  {
    x = 0;
    y = 0;
  } else 
  {
    r = 1.0f / r;
    x = r * cos(phi);
    y = r * sin(phi);
  }
  
  return Vec2f(x, y);
}


CINDER_APP_BASIC( Visualize_Superformula, RendererGl )

DOWNLOAD ALL CODE EXAMPLES

We are looking for implementations of the code examples in other programming languages to post on the site. If you would like to submit a sample, or if you find a bug, please write to

FORM+CODE in Design, Art, and Architecture

Visualize: SUPERFORMULA

Contributed Examples

ActionScript

OpenFrameworks

Cinder